Question

According to a report an average person watched 4.55 hours of television per day in 2005. A random sample of 20 people gave the following number of hours of television watched per day for last year. At the 10% significance level, do the data provide sufficient evidence to conclude that the amount of television watched per day last year by the average person differed from that in 2005? 1.0 4.6 5.4 3.7 5.2 1.7 6.1 1.9 7.6 9.1 6.9 5.5 9.0 3.9 2.5 2.4 4.7 4.1 3.7 6.2 a. identify the claim and state and b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic Sketch a graph decide whether to reject or fail to reject the null hypothesis, and d. interpret the decision in the context of the original claim. e. Obtain a 95%confidence interval

Answer 1

a. The claim is that the amount of television watched per day last year by the average person differed from that in 2005.

b. The critical values are tc=-1.729 and tc=1.729.

The acceptance region is defined by -1.792<t<1.729. See the picture attached.

c. Test statistic t=0.18.

The null hypothesis failed to be rejected.

d. At a significance level of 10%, there is not enough evidence to support the claim that the amount of television watched per day last year by the average person differed from that in 2005.

e. The 95% confidence interval for the mean is (2.29, 7.23).

Explanation:

We have a sample of size n=20, which has mean of 4.76 and standard deviation of 5.28.

`M=(1)/(n)\sum_(i=1)^n\,x_i\\\\\\M=(1)/(20)(1+4.6+5.4+. . .+6.2)\\\\\\M=(95.2)/(20)\\\\\\M=4.76\\\\\\s=(1)/(n-1)\sum_(i=1)^n\,(x_i-M)^2\\\\\\s=(1)/(19)((1-4.76)^2+(4.6-4.76)^2+(5.4-4.76)^2+. . . +(6.2-4.76)^2)\\\\\\s=(100.29)/(19)\\\\\\s=5.28\\\\\\`

a. This is a hypothesis test for the population mean.

The claim is that the amount of television watched per day last year by the average person differed from that in 2005.

Then, the null and alternative hypothesis are:

`H_0: \mu=4.55\\\\H_a:\mu\\eq 4.55`

The significance level is 0.1.

The sample has a size n=20.

The sample mean is M=4.76.

As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=5.28.

The estimated standard error of the mean is computed using the formula:

`s_M=(s)/(√(n))=(5.28)/(√(20))=1.181`

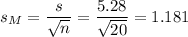
Then, we can calculate the t-statistic as:

`t=(M-\mu)/(s/√(n))=(4.76-4.55)/(1.181)=(0.21)/(1.181)=0.18`

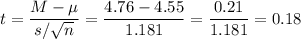
The degrees of freedom for this sample size are:

`df=n-1=20-1=19`

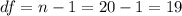
The critical value for a level of significance is α=0.10, a two tailed test and 19 degrees of freedom is tc=1.729.

The decision rule is that if the test statistic is above tc=1.729 or below tc=-1.729, the null hypothesis is rejected.

As the test statistic t=0.18 is within the critical values and lies in the acceptance region, the null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the amount of television watched per day last year by the average person differed from that in 2005.

We have to calculate a 95% confidence interval for the mean.

The population standard deviation is not known, so we have to estimate it from the sample standard deviation and use a t-students distribution to calculate the critical value.

The sample mean is M=4.76.

The sample size is N=20.

The standard error is s_M=1.181

The degrees of freedom for this sample size are df=19.

The t-value for a 95% confidence interval and 19 degrees of freedom is t=2.093.

The margin of error (MOE) can be calculated as:

`MOE=t\cdot s_M=2.093 \cdot 1.181=2.47`

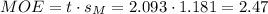
Then, the lower and upper bounds of the confidence interval are:

`LL=M-t \cdot s_M = 4.76-2.47=2.29\\\\UL=M+t \cdot s_M = 4.76+2.47=7.23`

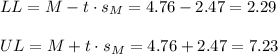
The 95% confidence interval for the mean is (2.29, 7.23).