Question

The radius r of a sphere is increasing at a rate of 3 inches per minute. (a) Find the rate of change of the volume when r = 9 inches. in.3/min (b) Find the rate of change of the volume when r = 37 inches. in.3/min

Answer 1

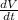`(dV)/(dt)` = 1017.87 in³/min

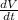`(dV)/(dt)` = 17203.35 in³/min

Explanation:

given data

radius r of a sphere is increasing at a rate = 3 inches per minute

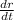`(dr)/(dt)` = 3

solution

we know volume of sphere is V =
`(4)/(3) \pi r^3`

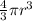
so
`(dV)/(dt) = (4)/(3) \pi r^2 (dr)/(dt)`

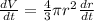
and when r = 9

so rate of change of the volume will be

rate of change of the volume
`(dV)/(dt) = (4)/(3) \pi (9)^2 (3)`

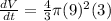
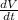`(dV)/(dt)` = 1017.87 in³/min

and

when r = 37 inches

so rate of change of the volume will be

rate of change of the volume
`(dV)/(dt) = (4)/(3) \pi (37)^2 (3)`

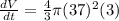
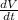`(dV)/(dt)` = 17203.35 in³/min