Question

Triangle ABC, with the vertices at A(0,0) B(3,5) and C(0,5) is graphed on the set of axes shown below. Name the solid that is formed when triangle ABC is rotated continuously about side AC and state the radius of the solid

Answer 1

Rotating triangle ABC about side AC forms a right circular cone with a base radius of 3 units.

Step-by-step explanation:

When triangle ABC, with vertices A(0,0), B(3,5), and C(0,5) is rotated continuously about side AC, the solid that is formed is called a right circular cone.

The side AC, being the axis of rotation, does not change its position. The other two sides of the triangle describe circles with their centers on the axis AC.

Since point B is at a distance of 3 units from the axis (the x-value of B), this describes the base of the cone. Hence, the base radius of the right circular cone is 3 units.

Answer 2

Solid formed will be a CONE

Radius of the cone = 3 units

Step-by-step explanation:

Given points of a triangle are A(0, 0), B(3, 5) and C(0, 5).

Given triangle is a right triangle.

When the given triangle ABC is rotated about a line AC, a 3D image of a solid will be created in the form of a CONE.

This cone will have the radius = BC

Length of side BC =
`√((y_2-y_1)^2+(x_2-x_1)^2)`

=
`√((3-0)^2+(5-5)^2)`

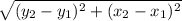
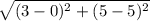
= 3

Therefore, radius of the cone = 3 units