Question

The average US house uses 10,972 kilowatt hours (kWh) in a year, an average of about 914 kWh per month. 1) hoover dammm produces about 4 billion kilowatt hours per year. How many houses can it power? 2) If the average (not hoover) dammm is 15 meters in height, how much water would have to drop out of the dam to power a house for a year?

Answer 1

1) 364,564 houses

2) Approximately 2.7 × 10⁸ litres of water annually

Step-by-step explanation:

The power consumption of the average household = 10,972 kWh/year

The power consumption,
`P_((consumed/house))` of the average household = 914 kWh/month

The amount of power produced,
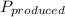`P_(produced)`, by the Hoover Dam = 4×10⁹ kW/year

1) The number of houses, n, the Hoover Dam can power is given by the relation;

`n = (P_(produced))/(P_((consumed/house))) = (4 * 10^9)/(10972) = 364,564.35 \ houses`

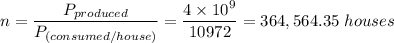
Which is approximately 364,564 houses

2) Given the height, h = 15 m

We have at 100% efficiency,

The potential energy of the water per year = 10,972 kWh

The potential energy of the water = m×g×h

Where:

g = Acceleration due to gravity = 9.81 m/s²

∴ The potential energy of the water = m×9.81×15

Therefore, we have;

m×9.81×15 = 10,972 kWh = 10972×60 min/hour ×60 seconds/minute Joules

m×9.81×15 = 39,499,200 kJ = 39,499,200,000 J

m = 39,499,200,000/(9.81 × 15) = 268,428,134.6 kg

The volume, V, of water that would have to drop out of the dam to power a house for a year is given by the relation;

Volume = (Mass of water)/(Density of water)

V = (268,428,134.6 kg)/(1000 kg/m³)

V = 268,428.135 m³ ≈ 2.7 × 10⁸ litres of water annually.