Question

An article suggests the uniform distribution on the interval (6.5, 19) as a model for depth (cm) of the bioturbation layer in sediment in a certain region.(a) What are the mean and variance of depth

Answer 1

The mean of depth is 12.75cm.

The variance of depth is of 13.02 cm².

Explanation:

An uniform probability is a case of probability in which each outcome is equally as likely.

For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.

The mean of the uniform distribution is:

`M = (a+b)/(2)`

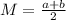
The variance of the uniform distribution is given by:

`V = ((b-a)^(2))/(12)`

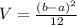
Uniform distribution on the interval (6.5, 19)

This means that:
`a = 6.5, b = 19`

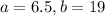
So

Mean:

`M = (6.5+19)/(2) = 12.75`

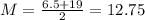
The mean of depth is 12.75cm.

Variance:

`V = ((19 - 6.5)^(2))/(12) = 13.02`

The variance of depth is of 13.02 cm².