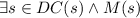Answer:
Explanation:
Recall the logic quantifiers
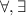 which means for all/for every and exists.
which means for all/for every and exists.
a) This means that for every student in D that is a computer science this implies that the student is not an engineering student. So for a student s in D such that C(s) then E(s) is false. This is symboled by
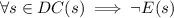
b) By saying "some computer science students" this means that there exists some studenst that study computer science and are also math majors. This is symboled by