Question

An aeroplane X whose average speed is 50°km/hr leaves kano airport at 7.00am and travels for 2 hours on a bearing 050°. It then changes its course and flies on a bearing 1200 to an airstrip A. Another aeroplane Y leaves kano airport at 10.00am and flies on a straight course to the airstrip A. both planes arrives at the airstrip A at 11.30am. calculate the average speed of Y to three significant figures. the direction of flight Y to the nearest degree

Answer 1

(a)123 km/hr

(b)39 degrees

Explanation:

Plane X with an average speed of 50km/hr travels for 2 hours from T (Kano Airport) to point U in the diagram.

Distance = Speed X Time

Therefore: Distance from T to U =50km/hr X 2 hr =100 km

It moves from Point U at 9.00 am and arrives at the airstrip A by 11.30am.

Distance, UA=50km/hr X 2.5 hr =125 km

Using alternate angles in the diagram:

`\angle U=110^\circ`

(a)First, we calculate the distance traveled, TA by plane Y.

Using Cosine rule

`u^2=t^2+a^2-2ta\cos U\\u^2=100^2+125^2-2(100)(125)\cos 110^\circ\\u^2=34175.50\\u=184.87$ km`

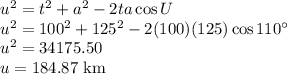
Plane Y leaves kano airport at 10.00am and arrives at 11.30am

Time taken =1.5 hour

Therefore:

Average Speed of Y

`=184.87 / 1.5\\=123.25$ km/hr\\\approx 123$ km/hr (correct to three significant figures)`

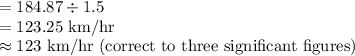
b)Flight Direction of Y

Using Law of Sines

`(t)/(\sin T) =(u)/(\sin U)\\(125)/(\sin T) =(184.87)/(\sin 110)\\123 * \sin T=125 * \sin 110\\\sin T=(125 * \sin 110) / 184.87\\T=\arcsin [(125 * \sin 110) / 184.87]\\T=39^\circ $ (to the nearest degree)`

The direction of flight Y to the nearest degree is 39 degrees.