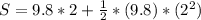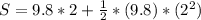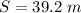Question

A soccer player is benched for being late to the game. In a fit of anger, she drops her ball from the top of the Physics building. It falls 4.9 meters after 1.0 second has elapsed. How much farther does it fall in the next 2.0 seconds

Answer 1

The distance is
`S = 39.2 \ m`

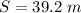
Step-by-step explanation:

From the question we are told that

The distance covered after t = 1 s is
`d = 4.9 \ m`

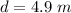
According to the equation of motion

`v^2 = u^2 + 2ad`

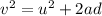
Now u = 0 m/s since before the drop the ball was at rest

`v^2 = 2ad`

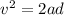
here
`a =g = 9.8 \ m/s^2`

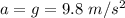
So

`v = 9.8 m/s`

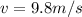
Also from equation of motion we have that

`S = ut + (1)/(2) at^2`

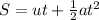
Now at t = 2 s , as given from the question

Then u = v = 9.8 m/s

And

`S = 9.8 * 2 + (1)/(2) * (9.8) * (2^2)`

`S = 9.8 * 2 + (1)/(2) * (9.8) * (2^2)`

`S = 39.2 \ m`