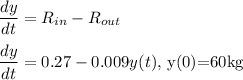Question

A tank contains 60 kg of salt and 1000 L of water. A solution of a concentration 0.03 kg of salt per liter enters a tank at the rate 9 L/min. The solution is mixed and drains from the tank at the same rate. Let y be the number of kg of salt in the tank after t minutes. Write the differential equation for this situation

Answer 1

`(dy)/(dt)=0.27-0.009y(t),$ y(0)=60kg`

Explanation:

Volume of water in the tank = 1000 L

Let y(t) denote the amount of salt in the tank at any time t.

Initially, the tank contains 60 kg of salt, therefore:

y(0)=60 kg

Rate In

A solution of concentration 0.03 kg of salt per liter enters a tank at the rate 9 L/min.

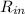`R_(in)` =(concentration of salt in inflow)(input rate of solution)

`=(0.03(kg)/(liter))( 9(liter)/(min))=0.27(kg)/(min)`

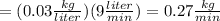
Rate Out

The solution is mixed and drains from the tank at the same rate.

Concentration,
`C(t)=(Amount)/(Volume) =(y(t))/(1000)`

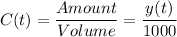
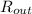`R_(out)` =(concentration of salt in outflow)(output rate of solution)

`=(y(t))/(1000)* 9(liter)/(min)=0.009y(t)(kg)/(min)`

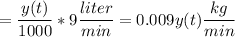
Therefore, the differential equation for the amount of Salt in the Tank at any time t:

`(dy)/(dt)=R_(in)-R_(out)\\\\(dy)/(dt)=0.27-0.009y(t),$ y(0)=60kg`