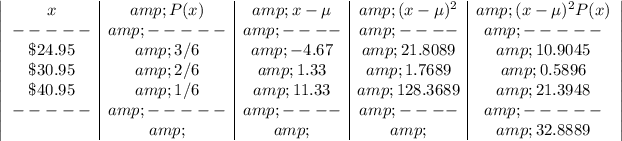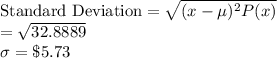Question

Internet Pricing An Internet Service Provider (ISP) offers its customers three options:

â Basic: Standard internet for everyday needs, at per month.
â Premium: Fast internet speeds for streaming video and downloading music, at per month.
â Ultra: Super-fast internet speeds for online gaming at per month.

Ultra is the company's least popular option; they have twice as many Premium customers, and three times as many Basic customers.


Required:
Let X be the monthly fee paid by a randomly selected customer. Give the probability distribution of X. Enter the exact answers.

Answer 1

(b)$29.62

(c)$5.73

Explanation:

Basic: Standard internet for everyday needs, at $24.95 per month.

Premium: Fast internet speeds for streaming video and downloading music, at $30.95 per month.

Ultra: Super-fast internet speeds for online gaming at $40.95 per month.

Let the number of customers on Ultra=x; therefore:

Number of Premium customers =2x

Number of Basic customers =3x

Total=x+2x+3x=6x

`P(Ultra)=(x)/(6x)=(1)/(6) \\P(Premium)=(2x)/(6x)=(1)/(3)\\P(Basic)=(3x)/(6x)=(1)/(2)`

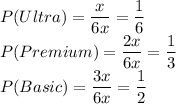
(a)X=Monthly fee paid by a randomly selected customer.

Therefore, the probability distribution of X is given as:

`\left|\begin{array}cX&P(X)\\---&---\\\$24.95&3/6\\\$30.95&2/6\\\$40.95&1/6\end{array}\right|`

(b)Average Monthly Revenue per customer

Mean,

`\mu=(\$24.95 * 3/6)+(\$30.95 * 2/6)+(\$40.95 * 1/6)\\=\$29.62`

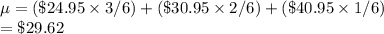
(c)Standard Deviation

`\left|\begin{array}cx&P(x)&x-\mu &(x-\mu)^2&(x-\mu)^2P(x)\\-----&-----&----&----&-----\\\$24.95&3/6&-4.67&21.8089&10.9045\\\$30.95&2/6&1.33&1.7689&0.5896\\\$40.95&1/6&11.33&128.3689&21.3948\\-----&-----&----&----&-----\\&&&&32.8889\end{array}\right|`

`\text{Standard Deviation}=√((x-\mu)^2P(x))\\=√(32.8889) \\ \sigma=\$5.73`