Complete Question
Samuel received $250 as prize money for winning the St. Peterson High School Badminton Tournament. The money was deposited in a special scholarship account that offered an annual interest of 1.8% compounded semiannually. The amount he will have in the accoutnt after t years can be calculated using the expression below.
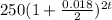
Use the given expression to complete the statements below.
The expression is the___(Product , Sum , Quotient , Square) of the amount initially deposited and the____(Quotient , Product , Difference , Sum) of one and the rate of increase raised to the number of ___.(Compounding Periods , Years, Months)
Answer:
- Product
- Sum
- Compounding Periods
Explanation:
For an amount invested at compound interest at a rate of r% with period for t years,
Amount
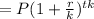
Comparing with the given expression:
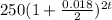
Period =2
Rate =0.018
Total Compounding Period =2 X t, where t=Number of years
Therefore:
The expression is the Product of the amount initially deposited and the Sum of one and the rate of increase raised to the number of Compounding Periods .