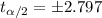Answer:
We want a confidence of 99% so then the significance level would be 1%
The degrees of freedom are given by:
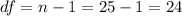
And the critical value using the significance level
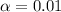 and
and
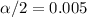 and the critical value would be:
and the critical value would be:
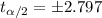
Explanation:
We know the following info :
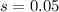 represent the standard deviation from the sample
represent the standard deviation from the sample
 represent the sample size selected
represent the sample size selected
We want a confidence of 99% so then the significance level would be 1%
The degrees of freedom are given by:
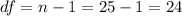
And the critical value using the significance level
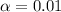 and
and
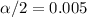 and the critical value would be:
and the critical value would be: