Answer:
Option D.
Explanation:
It is given that a triangle has side lengths 60 inches, 144 inches, 156 inches.
According to the Pythagoras theorem, in a right angle triangle

It means in a right angle triangle, square of largest side is equal to the sum of square of two smaller sides.
In the given triangle two smaller sides are 60 inches and 144 inches.

The largest side is 156 inches.
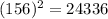
Since
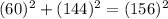 , so by Pythagoras theorem the given triangle is a right angle triangle.
, so by Pythagoras theorem the given triangle is a right angle triangle.
Therefore, the correct option is D.