Question

American adults are watching significantly less television than they did in previous decades. In 2016, Nielson reported that American adults are watching an average of five hours and twenty minutes, or 320 minutes, of television per day. 1. Find the probability that an average American adult watches more than 309 minutes of television per day. Answer in three decimal places. 2. Find the probability that an average American adult watches more than 2,250 minutes of television per week. Answer in three decimal places.

Answer 1

1. 0.271 = 27.1% probability that an average American adult watches more than 309 minutes of television per day.

2. 0.417 = 41.7% probability that an average American adult watches more than 2,250 minutes of television per week.

Explanation:

To solve this question, we need to understand the Poisson distribution and the normal distribution.

Poisson distribution:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\lambda)*\lambda^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\lambda` is the mean in the given interval, which is the same as the variance.

Normal distribution:

When the distribution is normal, we use the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

The Poisson distribution can be approximated to the normal with
`\mu = \lambda, \sigma = √(\lambda)`

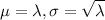
In 2016, Nielson reported that American adults are watching an average of five hours and twenty minutes, or 320 minutes, of television per day.

This means that
`\lambda = 320n`, in which n is the number of days.

1. Find the probability that an average American adult watches more than 309 minutes of television per day.

One day, so
`\mu = 320, \sigma = √(320) = 17.89`

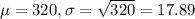
This probability is 1 subtracted by the pvalue of Z when X = 309. So

`Z = (X - \mu)/(\sigma)`

`Z = (309 - 320)/(17.89)`

`Z = 0.61`

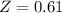
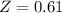`Z = 0.61` has a pvalue of 0.729

1 - 0.729 = 0.271

0.271 = 27.1% probability that an average American adult watches more than 309 minutes of television per day.

2. Find the probability that an average American adult watches more than 2,250 minutes of television per week.

`\mu = 320*7 = 2240, \sigma = √(2240) = 47.33`

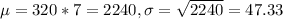
This is 1 subtracted by the pvalue of Z when X = 2250. So

`Z = (X - \mu)/(\sigma)`

`Z = (2250 - 2240)/(47.33)`

`Z = 0.21`

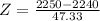
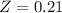
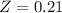`Z = 0.21` has a pvalue of 0.583

1 - 0.583 = 0.417

0.417 = 41.7% probability that an average American adult watches more than 2,250 minutes of television per week.