Question

A toy manufacturer wants to know how many new toys children buy each year. Assume a previous study found the standard deviation to be 1.8. She thinks the mean is 5.8 toys per year. What is the minimum sample size required to ensure that the estimate has an error of at most 0.12 at the 80% level of confidence

Answer 1

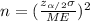`n=((z_(\alpha/2) \sigma)/(ME))^2` (b)

The critical value for 80% of confidence interval now can be founded using the normal distribution the significance level would be 20% and the critical value
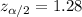`z_(\alpha/2)=1.28`, replacing into formula (b) we got:

`n=((1.28(1.8))/(0.12))^2 =368.64 \approx 369`

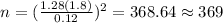
So the answer for this case would be n=369 rounded up to the nearest integer

Explanation:

We know the following info given:

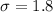`\sigma = 1.8` represent the standard deviation

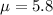`\mu = 5.8` the true mean that she believes

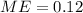`ME = 0.12` represent the margin of error

The margin of error is given by this formula:

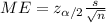`ME=z_(\alpha/2)(s)/(√(n))` (a)

And on this case we have that ME =+0.12 and we are interested in order to find the value of n, if we solve n from equation (a) we got:

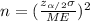`n=((z_(\alpha/2) \sigma)/(ME))^2` (b)

The critical value for 80% of confidence interval now can be founded using the normal distribution the significance level would be 20% and the critical value
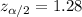`z_(\alpha/2)=1.28`, replacing into formula (b) we got:

`n=((1.28(1.8))/(0.12))^2 =368.64 \approx 369`

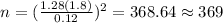
So the answer for this case would be n=369 rounded up to the nearest integer