Answer:
B, C and D
Explanation:
Given:
Statement: "Every integer has an additive inverse"
To find: statement that is equivalent to the given statement
Solution:
For any integer x, if
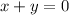 then y is the additive inverse of x.
then y is the additive inverse of x.
Here, 0 is the additive identity.
Statements ''All integers have additive inverses '', '' If x is an integer, then x has an additive inverse'' and ''Given an integer x, there exists a y such that y is the additive inverse of x'' are equivalent to the given statement "Every integer has an additive inverse".