Answer:
Approximately
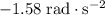 .
.
Step-by-step explanation:
This question suggests that the rotation of this object slows down "uniformly". Therefore, the angular acceleration of this object should be constant and smaller than zero.
This question does not provide any information about the time required for the rotation of this object to come to a stop. In linear motions with a constant acceleration, there's an SUVAT equation that does not involve time:
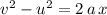 ,
,
where
 is the final velocity of the moving object,
is the final velocity of the moving object,
 is the initial velocity of the moving object,
is the initial velocity of the moving object,
 is the (linear) acceleration of the moving object, and
is the (linear) acceleration of the moving object, and
 is the (linear) displacement of the object while its velocity changed from
is the (linear) displacement of the object while its velocity changed from
 to
to
 .
.
The angular analogue of that equation will be:
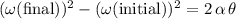 , where
, where
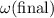 and
and
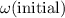 are the initial and final angular velocity of the rotating object,
are the initial and final angular velocity of the rotating object,
 is the angular acceleration of the moving object, and
is the angular acceleration of the moving object, and
 is the angular displacement of the object while its angular velocity changed from
is the angular displacement of the object while its angular velocity changed from
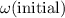 to
to
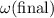 .
.
For this object:
 , whereas
, whereas
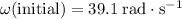 .
.
The question is asking for an angular acceleration with the unit
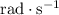 . However, the angular displacement from the question is described with the number of revolutions. Convert that to radians:
. However, the angular displacement from the question is described with the number of revolutions. Convert that to radians:
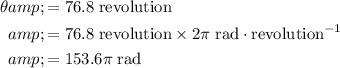 .
.
Rearrange the equation
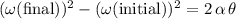 and solve for
and solve for
 :
:
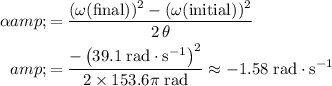 .
.