Question

We created this inequality to represent how Amy can meet her revenue goals:

-100x2 + 15,750x + 212,500 ≥ 243,600


In this activity, you’ll solve this inequality to find the minimum ticket price Amy should charge to meet her minimum revenue goal.


Part A

Set the inequality greater than or equal to 0.


Part B

Simplify the inequality by dividing by the GCF so the leading coefficient is positive.

Part C

Factor the left side of the inequality by grouping.

Part D

Solve the quadratic inequality. Remember to check any possible solutions for viability.

Part E

What is the minimum number of $2 increases that Amy needs to apply to the ticket price to reach her desired revenue?

Part F

What’s the minimum ticket price that Amy can charge and reach her goal? Recall that the ticket price is represented by 25 + 2x, where x represents the number of $2 increases.

Answer 1

Answer: B: 2x^2-315x+622_< 0

C: (2x-311)(x-2)_< 0

("_<" means greaten than for equal to)

Answer 2

x = 2

Price = $29

Explanation:

If x is the number of $2 dollars increases, then the minimum number of increases required to meet her goal is:

`-100x^2 + 15,750x + 212,500 \geq 243,600\\-100x^2 + 15,750x -31,100\geq 0\\x^2 -157.5x + 311\geq 0\\x=(157.5\pm√(157.5^2-(4*1*311)) )/(2)\\ x_1= 2\\x_2=155.5`

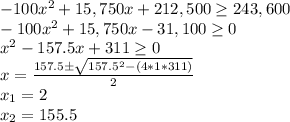
The only realistic value is x = 2 $2 increases

If the original price was $25, then the new rice required to reach Amy's goal is:

`P=25+2*2\\P=\$29`

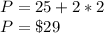
The minimum ticket price is $29.