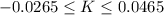Question

Silicon wafers are scored and then broken into the many small microchips that will he mounted into circuits. Two breaking methods are being compared. Out of 400 microchips broken by method A, 32 are unusable because of faulty breaks. Out of 400 microchips broken by method B, only 28 are unusable. Estimate the difference between proportions of improperly broken microchips for the two breaking methods. Use a confidence coefficient of 0.95. Which method of breaking would you recommend?

Answer 1

a

The estimate is
`- 0.0265\le K \le 0.0465`

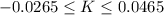
b

Method B this is because the faulty breaks are less

Explanation:

The number of microchips broken in method A is
`n_1 = 400`

The number of faulty breaks of method A is
`X_1 = 32`

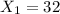
The number of microchips broken in method B is
`n_2 = 400`

The number of faulty breaks of method A is
`X_2 = 32`

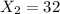
The proportion of the faulty breaks to the total breaks in method A is

`p_1 = (32)/(400)`

`p_1 = 0.08`

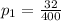
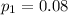
The proportion of the faulty to the total breaks in method B is

`p_2 = (28)/(400)`

`p_2 = 0.07`

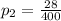
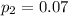
For this estimation the standard error is

`SE = \sqrt{ (p_1 (1 - p_1))/(n_1) + (p_2 (1- p_2 ))/(n_2) } }`

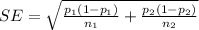
substituting values

`SE = \sqrt{ (0.08 (1 - 0.08))/(400) + (0.07 (1- 0.07 ))/(400) } }`

`SE = 0.0186`

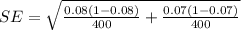
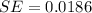
The z-values of confidence coefficient of 0.95 from the z-table is

`z_(0.95) = 1.96`

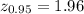
The difference between proportions of improperly broken microchips for the two breaking methods is mathematically represented as

`K = [p_1 - p_2 ] \pm z_(0.95) * SE`

substituting values

`K = [0.08 - 0.07 ] \pm 1.96 *0.0186`

`K = - 0.0265 \ or \ K = 0.0465`

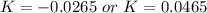
The interval of the difference between proportions of improperly broken microchips for the two breaking methods is

`- 0.0265\le K \le 0.0465`