Question

Circle V is shown. Line segments Y V and W V are radii. Tangents Y X and W X intersect at point X outside of the circle. The length of V Y is 5. Angle V is a right angle. What is the measure of circumscribed ∠X? 45° 50° 90° 95°

Answer 1

90

Explanation:

Answer 2

(C)
`90^\circ`

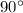
Explanation:

Theorem: The angle between a tangent and a radius is 90 degrees.

Given that

• YV and WV are radii
• YX and WX are tangent lines.

By the theorem stated above:

`\angle VYX =90^\circ\\\angle VWX =90^\circ`

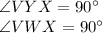
We are told that Angle V is a right angle.

Therefore, in the quadrilateral VWXY

`\angle VYX+\angle VWX+\angle V+ \angle X =360^\circ\\90^\circ+90^\circ+90^\circ+ \angle X =360^\circ\\270^\circ+ \angle X =360^\circ\\\angle X =360^\circ-270^\circ\\\angle X =90^\circ`

The measure of circumscribed ∠X is 90 degrees.