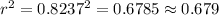Question

Calculate the coefficient of determination for the following data set. Round your answer to three decimal places. ACT Scores and College GPAs ACT Score, x College GPA, y 16 1.85 18 2.20 24 2.80 25 3.50 34 4.00 27 3.18 29 3.90 25 2.90 30 4.00 21 2.60 17 2.50 21 3.65 28 3.10 31 3.72 35 3.24 18 2.30 17 1.70 26 3.10 28 3.50 23 2.76

Answer 1

n=20
`\sum x = 493, \sum y = 60.5, \sum xy= 1553.01, \sum x^2 =12775, \sum y^2 =192.021`

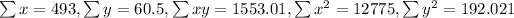
And in order to calculate the correlation coefficient we can use this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

`r=(20(1553.01)-(493)(60.5))/(√([20(12775) -(493)^2][20(192.021) -(60.5)^2]))=0.8237`

And then the determination coeffcient would be:

`r^2 = 0.8237^2= 0.6785 \approx 0.679`

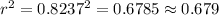
Explanation:

College GPAs ACT Score, x

16 18 24 25 34 27 29 25 30 21 17 21 28 31 35 18 17 26 28 23

College GPA, y

1.85 2.20 2.80 3.50 4.00 3.18 3.90 2.90 4.00 2.60 2.50 3.65 3.10 3.72 3.24 2.30 1.70 3.10 3.50 2.76

From the info given we can calculate the following sums:

n=20
`\sum x = 493, \sum y = 60.5, \sum xy= 1553.01, \sum x^2 =12775, \sum y^2 =192.021`

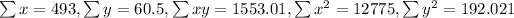
And in order to calculate the correlation coefficient we can use this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

`r=(20(1553.01)-(493)(60.5))/(√([20(12775) -(493)^2][20(192.021) -(60.5)^2]))=0.8237`

And then the determination coeffcient would be:

`r^2 = 0.8237^2= 0.6785 \approx 0.679`