Question

Which statement describes the behavior of the function f (x) = StartFraction 2 x Over 1 minus x squared EndFraction? f (x) = StartFraction 2 x Over 1 minus x squared EndFraction

Answer 1

The left hand end behavior is decreasing and approaching 0, while the right hand end behavior is increasing and approaching 0.

Explanation:

Assuming your fraction is
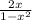`(2x)/(1-x^(2) )`, start by finding patterns. Since the denominator is 1-
`x^(2)`, we can see that any number that is not between 0 and 1 results in a negative denominator. The numerator is 2x, so when x>1, the function is negative, and when x<1, the function is positive.

The denominator can never equal 0 - that results in 1/0, which is an UNDEFINED number.

SO, x can never be -1 or 1.

There is a vertical asymptote where the denominator is 0, so z = -1 and zxx = 1 are vertical asymptotes.

As the denominator becomes larger, the number approaches 0.

The left hand end behavior is decreasing and approaching 0, while the right hand end behavior is increasing and approaching 0.

An easier way to determine end behavior in a shorter time frame is to substitute in large numbers and estimate... like estimating in 300 or 900

Answer 2

B. The graph approaches 0 as x approaches infinity.

Explanation:

The function f(x) is:

f(x) = (2x)/(1-x^2)

When x approach infinity the term x² grows rapidly (more rapid than x), thus 1 - x², which is in the denominator will decrease, become a large negative more rapid than the x in the numerator. Thus you can expect that the function approaches zero.