Question

The vertex of this parabola is at (2,-1). When the y value is 0, the value is 5.

What is the coefficient of the squared term in the parabola's equation?
(2.-1)
A.-3
B. -4
c. 4
D. 3

Answer 1

Option D.

Explanation:

The vertex form of a parabola along y-axis is

`y=a(x-h)^2+k`

where, (h,k) is vertex and, a is constant and it is equal to coefficient of the squared term in the parabola's equation.

The vertex of the parabola is (2,-1). So, h=2 and k=-1.

`y=a(x-2)^2-1`

The graph passes through (5,0). So,

`0=a(5-2)^2-1`

`1=9a`

`(1)/(9)=a`

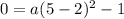
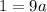
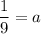
It means coefficient of the squared term is 1/9, which is not the option. So, parabola must be along the x-axis.

The vertex form of a parabola along x-axis is

`x=a(y-k)^2+h`

where, (h,k) is vertex and, a is constant and it is equal to coefficient of the squared term in the parabola's equation.

The vertex of the parabola is (2,-1). So, h=2 and k=-1.

`x=a(y+1)^2+2`

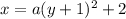
The graph passes through (5,0). So,

`5=a(0+1)^2+2`

`5-2=a`

`3=a`

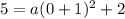
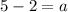
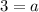
It means coefficient of the squared term is 3.

Therefore, the correct option is D.