Question

The mean number of hours of part-time work per week for a sample of 317 teenagers is 29. If the margin of error for the population mean with a 95% confidence interval is 2.1, construct a 95% confidence interval for the mean number of hours of part-time work per week for all teenagers.

Answer 1

The degrees of freedom are given by:

`df=n-1=317-1=316`

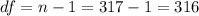
And replaicing we got:

`29-2.1=26.9`

`29+2.1=31.1`

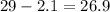
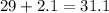
The 95% confidence interval would be between 26.9 and 31.1

Explanation:

Information given

`\bar X= 29` represent the sample mean

`\mu` population mean

s represent the sample standard deviation

`ME= 2.1` represent the margin of error

n represent the sample size

Solution

The confidence interval for the mean is given by the following formula:

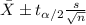`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

And this formula is equivalent to:

`\bar X \pm ME[/te]x</p><p>The degrees of freedom are given by:</p><p>[tex]df=n-1=317-1=316`

And replaicing we got:

`29-2.1=26.9`

`29+2.1=31.1`

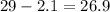
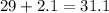
The 95% confidence interval would be between 26.9 and 31.1