Answer:

Where
 the relative growth is
the relative growth is
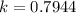 and t represent the number of days.
and t represent the number of days.
For this case we can to find the population after the day 6 so then we need to replace t =6 in our model and we got:
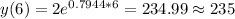
And for this case we can conclude that the population of protozoa for the 6 day would be approximately 235
Explanation:
We can assume that the following model can be used:

Where
 the relative growth is
the relative growth is
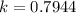 and t represent the number of days.
and t represent the number of days.
For this case we can to find the population after the day 6 so then we need to replace t =6 in our model and we got:
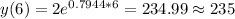
And for this case we can conclude that the population of protozoa for the 6 day would be approximately 235