Answer:
a)
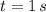 ,
,
 , b)
, b)
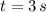 ,
,
 , c)
, c)
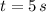 ,
,
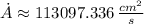 . The rate at which the area within the circle is increasing linearly inasmuch as time passes by.
. The rate at which the area within the circle is increasing linearly inasmuch as time passes by.
Explanation:
The area of a circle is described by the following formula:
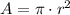
Where:
 - Area, measured in square centimeters.
- Area, measured in square centimeters.
 - Radius, measured in centimeters.
- Radius, measured in centimeters.
Since circular ripple is travelling outward at constant speed, radius can be described by the following equation of motion:

Where:
 - Speed of the circular ripple, measured in centimeters per second.
- Speed of the circular ripple, measured in centimeters per second.
 - Time, measured in seconds.
- Time, measured in seconds.
The rate of change of the circle is determined by deriving the equation of area and replacing radius with the function in terms of the speed of the circular ripple and time. That is to say:

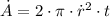
Where:
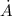 - Rate of change of the circular area, measured in square centimeters per second.
- Rate of change of the circular area, measured in square centimeters per second.
 - Speed of the circular ripple, measured in centimeters per second.
- Speed of the circular ripple, measured in centimeters per second.
 - Time, measured in seconds.
- Time, measured in seconds.
If
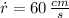 , then:
, then:
a)
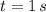
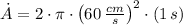

b)
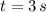


c)
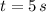
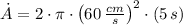
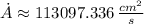
The rate at which the area within the circle is increasing linearly inasmuch as time passes by.