Question

compute an interval estimate with 90% confidence for the mean time to complete an employment test. Assuming a population standard deviation of three hours, what is the required sample size if the error should be less than a half hour

Answer 1

The required sample size 'n' = 97 .41 hours

Explanation:

Explanation:-

Given standard deviation of the Population 'σ' = 3 hours

Given the Margin of error =
`(1)/(2) hour`

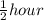
The Margin of error is determined by

`M.E = \frac{Z_{(\alpha )/(2) S.D} }{√(n) }`

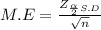
Given level of significance ∝ = 0.10 or 0.90

Z₀.₁₀ = 1.645

`(1)/(2) =(1.645 X 3)/(√(n) )`

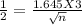
Cross multiplication , we get

`√(n) = 2 X 1.645 X 3`

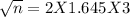
√n = 9.87

Squaring on both sides, we get

n = 97.41 hours

Final answer:-

The required sample size 'n' = 97.41 hours