Question

Jodie Meeks's Free Throws During the 2015-16 NBA season, Jodie Meeks of the Detroit Pistons had a free throw shooting percentage of 0.906 . Assume that the probability Jodie Meeks makes any given free throw is fixed at 0.906 , and that free throws are independent.If Jodie Meeks shoots 6 free throws in a game, what is the probability that he makes at least 5 of them?

Answer 1

0.8973

Explanation:

Relevant data provided in the question as per the question below:

Free throw shooting percentage = 0.906

Free throws = 6

At least = 5

Based on the above information, the probability is

Let us assume the X signifies the number of free throws

So, Then X ≈ Bin (n = 6, p = 0.906)

`P = (X = x) = $\sum\limits_(x)^6 (0.906)^x (1 - 0.906)^(6-x), x = 0,1,2,3,.., 6`

Now

The Required probability = P(X ≥ 5) = P(X = 5) + P(X = 6)

`= $\sum\limits_(5)^6 (0.906)^5 (1 - 0.906)^(6-5) + $\sum\limits_(6)^6 (0.906)^6 (1 - 0.906)^(6-6)`

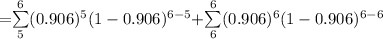
= 0.8973