Answer:
The power that fluid supplies to the turbine is 1752.825 kilowatts.
Step-by-step explanation:
A turbine is a device that works usually at steady state. Given that heat losses exists and changes in kinetic energy are not negligible, the following expression allows us to determine the power supplied by the fluid to the turbine by the First Law of Thermodynamics:
![-\dot Q_(loss) - \dot W_(out) + \dot m \cdot \left[(h_(in)-h_(out)) + (1)/(2)\cdot (v_(in)^(2)-v_(out)^(2)) \right] = 0](https://img.qammunity.org/2021/formulas/engineering/college/wkilrthhbxj8q72gn147h8u7lxqalr2d30.png)
Output power is cleared:
![\dot W_(out) = -\dot Q_(loss) + \dot m \cdot \left[(h_(in)-h_(out))+(1)/(2)\cdot (v_(in)^(2)-v_(out)^(2)) \right]](https://img.qammunity.org/2021/formulas/engineering/college/go1gdc1l22ktwdxr5yz5bouuomb7rex5hw.png)
If
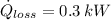 ,
,
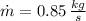 ,
,
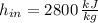 ,
,
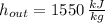 ,
,
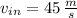 and
and
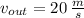 , then:
, then:
![\dot W_(out) = -0.3\,kW + \left(0.85\,(kg)/(s) \right)\cdot \left\{\left(2800\,(kJ)/(kg)-1550\,(kJ)/(kg) \right)+(1)/(2)\cdot \left[\left(45\,(m)/(s) \right)^(2)-\left(20\,(m)/(s) \right)^(2)\right] \right\}](https://img.qammunity.org/2021/formulas/engineering/college/lskhzygil3j5lods1kxe2idgl9xogkp38a.png)
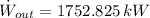
The power that fluid supplies to the turbine is 1752.825 kilowatts.