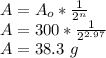Question

Calculate the amount of I - 125 that remains after 178.2 days if we started with 300 grams.

Answer 1

38.3 g

Step-by-step explanation:

The half life of a substance is the time taken for the substance to decay to about half of its amount.

Let us assume that I-125 have a half life of 60 days. It means that every 60 days, the amount of I - 125 would be halved.

The amount of I - 125 (A) that remains after t days is given by:

`A=A_o*(1)/(2^n) \\`

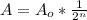
Where Ao is the initial amount and n = t / half life

Given that:

Ao = 300 g, t = 178.2 days.

Therefore n = t / half life = 178.2 days / 60 days = 2.97

`A=A_o*(1)/(2^n) \\A=300*(1)/(2^(2.97))\\ A=38.3\ g`