Answer:
Explanation:
1) first of all, let s check for n = 1
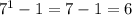
that s true
2) We assume that this is true for n
 is divisible by 6
is divisible by 6
what about
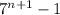 ?
?
we know that there is a k natural so that
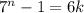
so
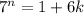
then
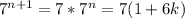
so

so it means that
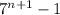 is divisible by 6
is divisible by 6
3) finally as this is true for n=1 and if this is true for n then it is true for n+1 we can conclude that
 is divisible by 6 for n positive integer
is divisible by 6 for n positive integer