Answer:
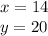
Explanation:
Finding x:
8x + 3x + 26 = 180 (Angle on a straight line add up to 180°)
11x = 180-26
11x = 154
Dividing both sides by 11
x = 14
Finding y:
3x + 5y + 38 = 180 (Angle on a straight line add up to 180°)
3(14) + 5y + 38 = 180
42 + 38 + 5y = 180
80 + 5y = 180
5y = 180-80
5y = 100
Dividing both sides by 5
y = 20