Answer:
B and E
Explanation:
Given the rational expression
 ← factorise the denominator
← factorise the denominator
2x² - 32 ← take out a common factor of 2 from each term
= 2(x² - 16) ← (x² - 16) is a difference of squares
= 2(x - 4)(x + 4)
The expression can now be written as
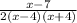
The denominator of the expression cannot be zero as this would make the expression undefined. Equating the denominator to zero and solving gives the values that x cannot be.
2(x - 4)(x + 4) = 0
Equate each factor to zero and solve for x
x - 4 = 0 ⇒ x = 4
x + 4 = 0 ⇒ x = - 4
These are the values of x that make the expression undefined.
x = 4 → B
x = - 4 → E