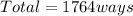Question

A company is looking to fill its Board of Directors position. 3 positions will be for men, 2

positions will be for women. There are 16 candidates, 9 men and 7 women. What is the
total possible outcome?

Answer 1

1764 ways

Explanation:

Given:

Men = 9

Women = 7

Required Men: 3

Required Women: 2

'

Required

Total Possible Outcome

The total possible outcome can be determine as follows;

Total = (Selection of Men) and (Selection of Women)

Calculating Selection of Men;

Let n represent total number of men; This implies that n = 9;

Let r represent number of men to select; This implies that r = 3;

The selection can be done in the following ways;

`Male = nCr`

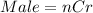
Where
`nCr = (n!)/(r!(n-r)!)`

`Male = 9C3`

`Male = (9!)/(3!(9-3)!)`

`Male = (9!)/(3!(6)!)`

`Male = (9 * 8 * 7 * 6!)/(3!6!)`

`Male = (9 * 8 * 7)/(3!)`

`Male = (9 * 8 * 7)/(3*2*1)`

`Male = 84 ways`

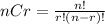
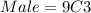
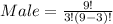
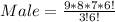
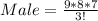
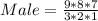
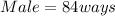
Calculating Selection of Women;

Let n represent total number of men; This implies that n = 7;

Let r represent number of men to select; This implies that r = 2;

The selection can be done in the following ways;

`Female = nCr`

Where
`nCr = (n!)/(r!(n-r)!)`

`Female = 7C2`

`Female = (7!)/(2!(7-2)!)}`

`Female = (7!)/(2!(5)!)`

`Female = (7 * 6 * 5!)/(2!5!)`

`Female = (7 * 6)/(2!)`

`Female = (42)/(2*1)`

`Female = 21 ways`

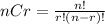
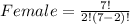
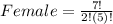
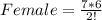
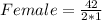
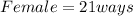
Recall that

Total = (Selection of Men) and (Selection of Women)

Hence,

`Total = 84 * 21`

`Total = 1764 ways`