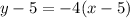Answer:
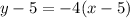
Explanation:
Given
Line coordinates: (5,5)
Perpendicular slope =

Required
Find the point slope form of the line
First, the slope of the line has t be calculated;
Given that two lines are perpendicular;
The relationship between there slopes is given as
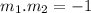
Let m_2 represent the slope of the second line;
such that

So;
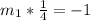
Multiply both sides by 4
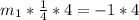
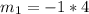
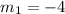
Now, the equation of the line can be calculated using slope formula;

Where
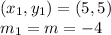
So;
 becomes
becomes
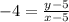
Multiply both sides by x - 5
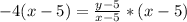
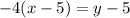
Reorder
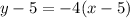
Hence, the line in point-slope form is