Question

In a random sample of six cell​ phones, the mean full retail price was ​$538.00 and the standard deviation was ​$184.00. Assume the population is normally distributed and use the​ t-distribution to find the margin of error and construct a 90​% confidence interval for the population mean mu. Interpret the results. Identify the margin of error. Construct a 90​% confidence interval for the population mean. Interpret the results. Select the correct choice below and fill in the answer box to complete your choice.

Answer 1

The margin of error is 370.8.

The 90​% confidence interval for the population mean is between $167.2 and $908.8

The correct interpretation is that we are 90% sure that the true mean price for all cellphones in within the interval end-points, so option B.

Explanation:

The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So

df = 6 - 1 = 5

90% confidence interval

Now, we have to find a value of T, which is found looking at the t table, with 5 degrees of freedom(y-axis) and a confidence level of
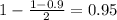`1 - (1 - 0.9)/(2) = 0.95`. So we have T = 2.0150

The margin of error is:

M = T*s = 2.0150*184 = 370.8.

In which s is the standard deviation of the sample.

The lower end of the interval is the sample mean subtracted by M. So it is 538 - 370.8 = $167.2

The upper end of the interval is the sample mean added to M. So it is 538 + 370.8 = $908.8

The 90​% confidence interval for the population mean is between $167.2 and $908.8

The correct interpretation is that we are 90% sure that the true mean price for all cellphones in within the interval end-points, so option B.