Answer:
Option B
Explanation:
Let us consider that these right triangles form a sort of proportion among one another. If that is so, we can list out which sides of one triangle correspond to which side of the other triangle;
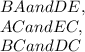
With this being said, it is given that BA = 84, and DE = 7. To prove that the could be proportional, let us form a like fraction;
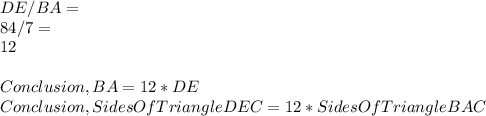
With that, the length of AC in respect to EC can be represented as such;
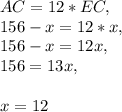
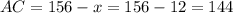
Solution - Option B