Question

An insulated rigid tank is divided into two equal parts by a partition. Initially, one part contains 4 kg of an ideal gas at 750 kPa and 48°C, and the other part is evacuated. The partition is now removed, and the gas expands into the entire tank. Determine the final temperature and pressure in the tank. (Round the final answers to the nearest whole number.)

Answer 1

The final temperature and pressure in the insulated rigid tank are
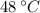`48\,^(\circ)C` and
`375\,kPa`.

Step-by-step explanation:

An ideal gas is represented by the following model:

`P\cdot V = (m)/(M)\cdot R_(u) \cdot T`

Where:

`P` - Pressure, measured in kilopascals.

`V` - Volume, measured in cubic meters.

`m` - Mass of the ideal gas, measured in kilograms.

`M` - Molar mass, measured in kilograms per kilomole.

`T` - Temperature, measured in Kelvin.

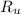`R_(u)` - Universal constant of ideal gases, equal to
`8.314\,(kPa\cdot m^(3))/(kmol\cdot K)`

As tank is rigid and insulated, it means that no volume deformations in tank, heat and mass interactions with surroundings occur during expansion process. Hence, final pressure is less that initial one, volume is doubled (due to equal partitioning) and temperature remains constant. Hence, the following relationship can be derived from model for ideal gases:

`(P_(1)\cdot V_(1))/(T_(1)) = (P_(2)\cdot V_(2))/(T_(2))`

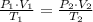
Now, final pressure is cleared:

`P_(2) = P_(1)\cdot (T_(2))/(T_(1))\cdot (V_(1))/(V_(2))`

`P_(2) = (750\,kPa)\cdot 1 \cdot (1)/(2)`

`P_(2) = 375\,kPa`

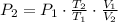
The final temperature and pressure in the insulated rigid tank are
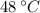`48\,^(\circ)C` and
`375\,kPa`.