Question

To study the properties of various particles, you can accelerate the particles with electric fields. A positron is a particle with the same mass as an electron but the opposite charge ( e). If a positron is accelerated by a constant electric field of magnitude 286 N/C, find the following.

(a) Find the acceleration of the positron. m/s2
(b) Find the positron's speed after 8.70 × 10-9 s. Assume that the positron started from rest. m/s

Answer 1

a) a = 5.03x10¹³ m/s²

b)
`V_(f) = 4.4 \cdot 10^(5) m/s`

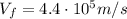
Explanation:

a) The acceleration of the positron can be found as follows:

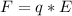`F = q*E` (1)

Also,

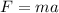`F = ma` (2)

By entering equation (1) into (2), we have:

`a = (F)/(m) = (qE)/(m)`

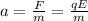
Where:

F: is the electric force

m: is the particle's mass = 9.1x10⁻³¹ kg

q: is the charge of the positron = 1.6x10⁻¹⁹ C

E: is the electric field = 286 N/C

`a = (qE)/(m) = (1.6 \cdot 10^(-19) C*286 N/C)/(9.1 \cdot 10^(-31) kg) = 5.03 \cdot 10^(13) m/s^(2)`

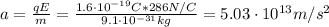
b) The positron's speed can be calculated using the following equation:

`V_(f) = V_(0) + at`

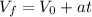
Where:

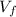`V_(f)`: is the final speed =?

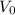`V_(0)`: is the initial speed =0

t: is the time = 8.70x10⁻⁹ s

`V_(f) = V_(0) + at = 0 + 5.03 \cdot 10^(13) m/s^(2)*8.70 \cdot 10^(-9) s = 4.4 \cdot 10^(5) m/s`

I hope it helps you!