Question

Three blocks are placed in contact on a horizontal frictionless surface. A constant force of magnitude F is applied to the box of mass M. There is friction between the surfaces of blocks 2M and 3M so the three blocks accelerate together to the right.

Which block has the smallest net force acting on it?
A) M
B) 2M
C) 3M
D) The net force is the same for all three blocks Submit

Answer 1

A) M

Step-by-step explanation:

The three blocks are set in series on a horizontal frictionless surface, whose mutual contact accelerates all system to the same value due to internal forces as response to external force exerted on the box of mass M (Newton's Third Law). Let be F the external force, and F' and F'' the internal forces between boxes of masses M and 2M, as well as between boxes of masses 2M and 3M. The equations of equilibrium of each box are described below:

Box with mass M

`\Sigma F = F - F' = M\cdot a`

Box with mass 2M

`\Sigma F = F' - F'' = 2\cdot M \cdot a`

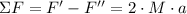
Box with mass 3M

`\Sigma F = F'' = 3\cdot M \cdot a`

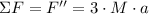
On the third equation, acceleration can be modelled in terms of F'':

`a = (F'')/(3\cdot M)`

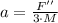
An expression for F' can be deducted from the second equation by replacing F'' and clearing the respective variable.

`F' = 2\cdot M \cdot a + F''`

`F' = 2\cdot M \cdot \left((F'')/(3\cdot M) \right) + F''`

`F' = (5)/(3)\cdot F''`

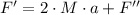
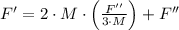
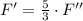
Finally, F'' can be calculated in terms of the external force by replacing F' on the first equation:

`F - (5)/(3)\cdot F'' = M \cdot \left((F'')/(3\cdot M) \right)`

`F = (5)/(3) \cdot F'' + (1)/(3)\cdot F''`

`F = 2\cdot F''`

`F'' = (1)/(2)\cdot F`

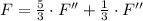
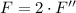
Afterwards, F' as function of the external force can be obtained by direct substitution:

`F' = (5)/(6)\cdot F`

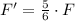
The net forces of each block are now calculated:

Box with mass M

`M\cdot a = F - (5)/(6)\cdot F`

`M\cdot a = (1)/(6)\cdot F`

Box with mass 2M

`2\cdot M\cdot a = (5)/(6)\cdot F - (1)/(2)\cdot F`

`2\cdot M \cdot a = (1)/(3)\cdot F`

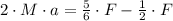
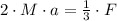
Box with mass 3M

`3\cdot M \cdot a = (1)/(2)\cdot F`

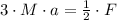
As a conclusion, the box with mass M experiments the smallest net force acting on it, which corresponds with answer A.