Question

There are ​$400 available to fence in a rectangular garden. The fencing for the side of the garden facing the road costs ​$15 per​foot, and the fencing for the other three sides costs ​$5 per foot. Consider the problem of finding the dimensions of the largest possible garden.​(a) what would be the objective equation and what would be the constraint equations?​(b) Express the quantity to be maximized as a function of x.​(c) Find the optimal values of x and y.

Answer 1

The answer to this question can be described as follows:

Explanation:

A)

The goal is to increase the area and therefore

Target formula: A = xy

The limited amount of money, which we have for the fence, and it only has $400

The equation of constraints: 400=(fence costs parallel to roads) +( 3 other side cost)

`\to 400 = 15x+ 5(5y+x)\\\\ \to400 =15x+25y+5x\\\\ \to 400=20x+25y\\`

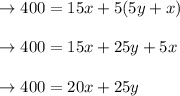
B)

To solve y we use the limiting equation:

`\to 400=20x+25y\\\\ \to 25y= 400-20x\\\\\to y=((400-20x)))/(25)\\\\\to y=16-(4)/(5)x\\\\`

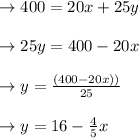
Now, put the value in the y and maximise as much as possible into our goal equation:

A function for:

`\to A(x)= x(16-((4)/(5)x)\\\\\to A(x) =16x-(4x^2)/(5)`

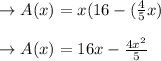
C)

Select the critical value the A(x):

`\to (dA)/(dx) 16-(8x)/(5)=0 \\\\\to 16=(8x)/(5)\\\\\to 16 * 5 =8x\\\\\to 80=8x \\\\\to x=(80)/(8)\\\\\to x=10\\\\`

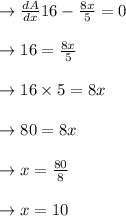
We now need, with the second derivative, to ensure that this value is maximum:

`\to (d^2A)/(dx^2) = (-8)/(5)\\\\ \to (d^2A)/(dx^2)(10) < O`

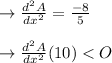
not only is there a relative maximum at x = 10, but we can conclude that the

maximum occurs as
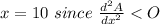`x = 10 \ since \ (d^2A)/(dx^2)< O` for all x. We also need y:

`\to y= 16-(4)/(5)x\\\\\to y=16-(4)/(5)*10\\\\\to y= 16-8\\\\\to y=8\\\\`