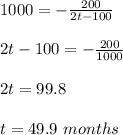Answer:
Suppose a population of rodents satisfies the differential equation dP 2 kP dt = . Initially there are P (0 2 ) = rodents, and their number is increasing at the rate of 1 dP dt = rodent per month when there are P = 10 rodents.
How long will it take for this population to grow to a hundred rodents? To a thousand rodents?
Explanation:
Use the initial condition when dp/dt = 1, p = 10 to get k;
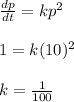
Seperate the differential equation and solve for the constant C.
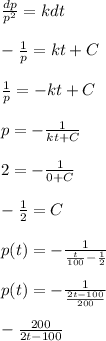
You have 100 rodents when:
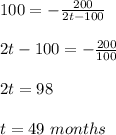
You have 1000 rodents when: