Answer:
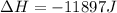
Step-by-step explanation:
Hello,
In this case, it is widely known that for isochoric processes, the change in the enthalpy is computed by:
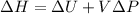
Whereas the change in the internal energy is computed by:
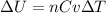
So we compute the initial and final temperatures for one mole of the ideal gas:
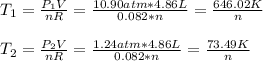
Next, the change in the internal energy, since the volume-constant specific heat could be assumed as ³/₂R:
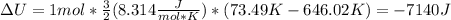
Then, the volume-pressure product in Joules:
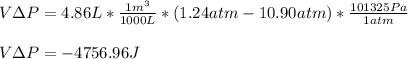
Finally, the change in the enthalpy for the process:
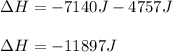
Best regards.