Answer:
6.3 rev/s
Step-by-step explanation:
The new rotation rate of the satellite can be found by conservation of the angular momentum (L):
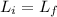
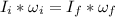
The initial moment of inertia of the satellite (a solid sphere) is given by:
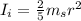
Where
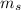 : is the satellite mass and r: is the satellite's radium
: is the satellite mass and r: is the satellite's radium
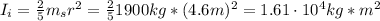
Now, the final moment of inertia is given by the satellite and the antennas (rod):
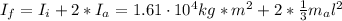
Where
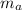 : is the antenna's mass and l: is the lenght of the antenna
: is the antenna's mass and l: is the lenght of the antenna
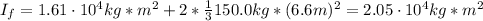
So, the new rotation rate of the satellite is:
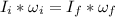
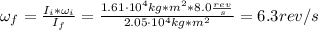
Therefore, the new rotation rate of the satellite is 6.3 rev/s.
I hope it helps you!