Question

A survey showed that 79% of adults need correction (eyeglasses, contacts, surgery, etc.) for their eyesight. If 16 adults are randomly selected,

find the probability that no more than 1 of them need correction for their eyesight. Is 1 a significantly low number of adults requiring eyesight
correction?
The probability that no more than 1 of the 16 adults require eyesight correction is
(Round to three decimal places as needed.)

Answer 1

P (X≤1) = 0.000

Explanation:

Data given:

p = 79% = 0.79

q = 1 - 0.79 = 0.21

n = 16

P (no more than 1 in 16 adults) = P (X≤1)

P (X≤1) = P (X=0) + P (X=1)

We can find the probability by using binomial functions:

`P=(n!)/(x!(n-x)!)p^x(1-p)^(n-x)`

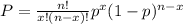
P(X=0):

P(X=0) = (16! / 0!(16-0)!) · 0.79⁰ · 0.21¹⁶

Use calculator to solve:

P(X=0) = 0.000000000798

P(X=1):

P(X=1) = (16! / 1!(16-1)!) · 0.79¹ · 0.21¹⁵

Use calculator to solve:

P(X=1) = 0.000000034506

P(X≤1)

P (X≤1) = P (X=0) + P (X=1)

P (X≤1) = 0.000000000798 + 0.000000034506

P (X≤1) = 0.00000003530

P (X≤1) = 0.000

As 1 is a very low number, its probability is very small