Question

Suppose that we want to generate the outcome of the flip of a fair coin, but that all we have at our disposal is a biased coin which lands on heads with some unknown probability p that need not be equal to1/2. Consider the following procedure for accomplishing our task:

1. Flip the coin.
2. Flip the coin again.
3. If both flips land on heads or both land on tails, return to step 1. 4. Let the result of the last flip be the result of the experiment.
(a) Show that the result is equally likely to be either heads or tails.
(b) Could we use a simpler procedure that continues to flip the coin until the last two flips are different and then lets the result be the outcome of the final flip?

Answer 1

Explanation:

Given that;

the following procedure for accomplishing our task are:

1. Flip the coin.

2. Flip the coin again.

From here will know that the coin is first flipped twice

3. If both flips land on heads or both land on tails, it implies that we return to step 1 to start again. this makes the flip to be insignificant since both flips land on heads or both land on tails

But if the outcomes of the two flip are different i.e they did not land on both heads or both did not land on tails , then we will consider such an outcome.

Let the probability of head = p

so P(head) = p

the probability of tail be = (1 - p)

This kind of probability follows a conditional distribution and the probability of getting heads is :

`P( \{Tails, Heads\})|\{Tails, Heads,( Heads ,Tails)\})`

`= \frac{P( \{Tails, Heads\}) \cap \{Tails, Heads,( Heads ,Tails)\})}{ {P( \{Tails, Heads,( Heads ,Tails)\}}}`

`= \frac{P( \{Tails, Heads\}) }{ {P( \{Tails, Heads,( Heads ,Tails)\}}}`

`= \frac{P( \{Tails, Heads\}) } { {P( Tails, Heads) +P( Heads ,Tails)}}`

`=((1-p)*p)/((1-p)*p+p*(1-p))`

`=((1-p)*p)/(2(1-p)*p)`

`=(1)/(2)`

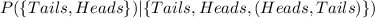
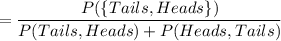
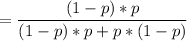
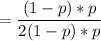
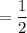
Thus; the probability of getting heads is
`(1)/(2)` which typically implies that the coin is fair

(b) Could we use a simpler procedure that continues to flip the coin until the last two flips are different and then lets the result be the outcome of the final flip?

For a fair coin (0<p<1) , it's certain that both heads and tails at the end of the flip.

The procedure that is talked about in (b) illustrates that the procedure gives head if and only if the first flip comes out tail with probability 1 - p.

Likewise , the procedure gives tail if and and only if the first flip comes out head with probability of p.

In essence, NO, procedure (b) does not give a fair coin flip outcome.