Question

Chords AB and CD intersect inside a circle at point E. AE= 2, CE =4 , and ED =3 . Find EB.

Answer 1

EB = 6 units

Explanation:

It is given that we have a circle and two cords AB and CD inside that circle.

AB and CD intersect each other at point E.

Also the values of AE, CE and ED are as follows:

AE = 2 units

CE = 4 units

ED = 3 units

To find: EB = ?

Please refer to the figure attached for a clear picture of the given dimensions.

The relation between intersecting cords is given as:

If the two cords are intersecting and they are divided in parts a, b and c,d

Then

a
`*` b = c
`*` d

Here,

a = AE = 2 units

c = CE = 4 units

d = ED = 3 units

b = EB = ?

Putting the values in formula:

2
`*` EB = 3
`*` 4

`\Rightarrow EB = (12)/(2)\\\Rightarroe EB = 6\ units`

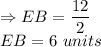
So, the answer is EB = 6 units