Answer:
At the end of ten days, the size of population B is 256 times that of population A
Explanation:
We work under the premise that population A and B start both with the same number of individuals. Let's call such initial population

Now, we write the exponential expression that describes population A as a function of days (t) for the first 6 days:
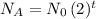
which represents the starting point with
 individuals on day zero, doubling after one day (t= 1), and keeping on doubling the following days for 6 days.
individuals on day zero, doubling after one day (t= 1), and keeping on doubling the following days for 6 days.
So at the end of 6 days, population A would have the following number of individuals:
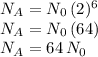
That is 64 times the starting number of individuals.
After this, the population stops growing and starts reducing to one-half each day. This behavior can be represented by:
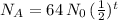
therefore after 4 days in this pattern, this culture has the following number of organisms:
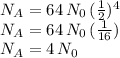
which is now just four times what the culture started with.
Now, on the other hand, population B grows doubling each day without interruption, so at the end of 10 days its size is given by:

that is it has 1024 times the initial number of organisms.
So if we compare both populations at day 10:
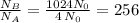
Therefore, at the end of ten days, population B is 256 times the size of population A