Question

Find the volume of the solid shown or described. If necessary, round to the nearest tenth. What is the volume of the shed?

Answer 1

Based on the calculations, the volume of the shed equal to: B. 38
`m^3`.

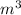By critically observing the solid shown above, we can logically deduce that the base of the prism represents the front face of the shed while the height of the prism is represented by the 2 meters distance between the front base and the back base.

Additionally, the front base comprises a rectangle with length 5 meters and width 3 meters, and a triangle with base 5 meters and height 1.6 meters.

Area of base = area of rectangle + area of triangle

Area of base = LW + (1/2)bh

Area of base = (5 × 3) + 1/2 × 5 × 1.6

Area of base = 15 + 4

Area of base = 19 square meters.

Volume of shed = area of base × height

Volume of shed = 19 × 2

Volume of shed = 38 cubic meters.

Answer 2

Option (B)

Explanation:

Given shed is a composite figure having a rectangular solid at the base and a triangular prism on the top.

Volume of the shed = Volume of the rectangular prism + Volume of the triangular prism

Volume of the rectangular prism = length × width × height

= 5 × 2 × 3

= 30 m³

Volume of the triangular prism = Area of the base × height of the prism

=
`(1)/(2)(\text{Base})(\text{height of the triangular bsae})` × height of the prism

=
`[(1)/(2)(5)(1.6)]* 2`

= 8 m³

Volume of the shed = volume of the rectangular prism + volume of the triangular prism

= 30 + 8

= 38 m³

Therefore, Option (B) will be the answer.