Question

An object, with mass 70 kg and speed 21 m/s relative to an observer, explodes into two pieces, one 4 times as massive as the other; the explosion takes place in deep space. The less massive piece stops relative to the observer. How much kinetic energy is added to the system during the explosion, as measured in the observer's reference frame

Answer 1

K = 3.9 kJ

Step-by-step explanation:

The kinetic energy (
`K_(T)`) added is given by the difference between the final kinetic energy and the initial kinetic energy:

`K_(T) = K_(f) - K_(i)`

The initial kinetic energy is:

`K_(i) = (1)/(2)m_(1)v_(1)^(2)`

Where m₁ is the mass of the object before the explosion and v₁ is its velocity

`K_(i) = (1)/(2)m_(1)v_(1)^(2) = (1)/(2)70 kg*(21 m/s)^(2) = 1.54 \cdot 10^(4) J`

Now, the final kinetic energy is:

`K_(f) = (1)/(2)m_(2)v_(2)^(2) + (1)/(2)m_(3)v_(3)^(2)`

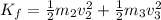
Where m₂ and m₃ are the masses of the 2 pieces produced by the explosion and v₁ and v₂ are the speeds of these pieces

Since m₂ is 4 times as massive as m₃ and v₃ = 0, we have:

`K_(f) = (1)/(2)*(4)/(5)m_(1)v_(2)^(2) + (1)/(2)*(1)/(5)m_(1)*0` (1)

By conservation of momentum we have:

`p_(i) = p_(f)`

`m_(1)v_(1) = m_(2)v_(2) + m_(3)v_(3)`

`m_(1)v_(1) = (4)/(5)m_(1)v_(2) + (1)/(5)m_(1)*0`

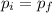
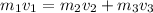
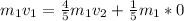
`v_(2) = (5)/(4)v_(1)` (2)

By entering (2) into (1) we have:

`K_(f) = (1)/(2)*(4)/(5)m_(1)((5)/(4)v_(1))^(2) = (1)/(2)*(4)/(5)70 kg((5)/(4)*21 m/s)^(2) = 1.93 \cdot 10^(4) J`

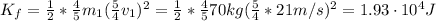
Hence, the kinetic energy added is:

`K_(T) = K_(f) - K_(i) = 1.93 \cdot 10^(4) J - 1.54 \cdot 10^(4) J = 3.9 \cdot 10^(3) J`

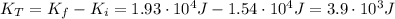
Therefore, the kinetic energy added to the system during the explosion is 3.9 kJ.

I hope it helps you!